Back مسألة التسطيح Arabic Flachheitsproblem German Problema de planitud Spanish Tasasuse probleem Estonian مسئله تخت‌بودن Persian Problème de la platitude French 平坦性問題 Japanese 편평도 문제 Korean Vlak heelal Dutch Problem płaskości Polish

Flatness problem

The local geometry of the universe is determined by whether the relative density Ω is less than, equal to or greater than 1. From top to bottom: a spherical universe with greater than critical density (Ω>1, k>0); a hyperbolic, underdense universe (Ω<1, k<0); and a flat universe with exactly the critical density (Ω=1, k=0). The spacetime of the universe is, unlike the diagrams, four-dimensional.

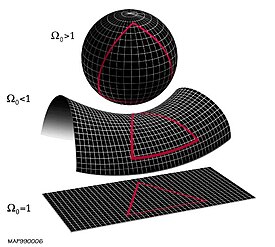
The flatness problem (also known as the oldness problem) is a cosmological fine-tuning problem within the Big Bang model of the universe. Such problems arise from the observation that some of the initial conditions of the universe appear to be fine-tuned to very 'special' values, and that small deviations from these values would have extreme effects on the appearance of the universe at the current time.

In the case of the flatness problem, the parameter which appears fine-tuned is the density of matter and energy in the universe. This value affects the curvature of space-time, with a very specific critical value being required for a flat universe. The current density of the universe is observed to be very close to this critical value. Since any departure of the total density from the critical value would increase rapidly over cosmic time,[1] the early universe must have had a density even closer to the critical density, departing from it by one part in 1062 or less. This leads cosmologists to question how the initial density came to be so closely fine-tuned to this 'special' value.

The problem was first mentioned by Robert Dicke in 1969.[2]: 62,  [3]: 61  The most commonly accepted solution among cosmologists is cosmic inflation, the idea that the universe went through a brief period of extremely rapid expansion in the first fraction of a second after the Big Bang; along with the monopole problem and the horizon problem, the flatness problem is one of the three primary motivations for inflationary theory.[4]

  1. ^ Peacock, J. A. (1998). Cosmological Physics. Cambridge: Cambridge University Press. ISBN 978-0-521-42270-3.
  2. ^ Robert H. Dicke (1970). Gravitation and the Universe: Jayne Lectures for 1969. American Philosophical Society. ISBN 978-0871690784.
  3. ^ Alan P. Lightman (1 January 1993). Ancient Light: Our Changing View of the Universe. Harvard University Press. ISBN 978-0-674-03363-4.
  4. ^ Ryden, Barbara (2002). Introduction to Cosmology. San Francisco: Addison Wesley. ISBN 978-0-8053-8912-8.

Rich TVX News Network Site

Rich TVX News Network Info

© MMXXIII Rich X Search. We shall prevail. All rights reserved. Rich X Search